Michael Schaub

Michael Schaub

Computational Network Science @RWTH Aachen University

HIntNets: Higher-order interactions and Laplacian dynamics in complex networks: structure, dynamics and control

image-right Marie Skłodowska-Curie Individual Fellowships
(MSCA-IF-GF - Global Fellowships, Project ID: 702410)

This page collects information about the project “HIntNets”.
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 702410.

Overview

Complex networks are an essential ingredient of modern life, and underpin integral parts of our biological, physical, technological and socio-economic universe. Thus far, such networks have been mainly represented as graphs. However, while graphs can capture pairwise interactions between nodes, fundamental interactions in networks often take place between multiple nodes. For example, in socio-economic networks, the joint coordinated activity of several agents (e.g., buyer, seller, broker); the formation and interactions of coalitions; the emergence of peer pressure; and the existence of triadic closure are all prevalent.

To investigate such group interactions in complex networks and their dynamical implications is the main objective of this interdisciplinary project. Specifically, we will investigate how such interactions can be taken into account for modelling, analysis and design of complex networks, and will investigate generalized network models. While in some cases data about group interactions is readily available, in many cases the groupings or even the network of interactions might be unknown. We will thus further investigate techniques to infer (generalized) networks and group structures from available interaction data.

The overarching goal of this research is to elucidate relations between structure, dynamics and function in complex systems. See the video above produced in the context of this project for a high-level introduction to the topic.

Events

Sep 9 - 11, 2019, Workshop on Higher-Order Interaction Networks: Dynamics, Structure, Data
May 28, 2019, Workshop on Higher-Order Models in Network Science HONS 2019 (part of Netsci 2019).
June 12, 2018, Workshop on Higher-Order Models in Network Science HONS 2018 (part of Netsci 2018).

Selected Projects

Simplicial Complexes as modelling tools for complex systems

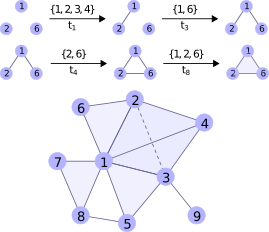image-right To integrate higher order interactions into network models, a framework is needed to extend standard graph based approaches. Hypergraphs can provide such a general framework. We concentrate on a particular form of hypergraphs called simplicial complexes (SCs), i.e., finite collections of simplices (nodes, edges, triangular faces, etc.) closed under intersections. We show how simplicial complexes can be used as a natural data model for a variety of systems, study their temporal evolution, and introduce higher-order link prediction as a benchmark problem to assess models and algorithms that predict higher-order structure [1].

Compared to generic hypergraphs, SC have favourable additional algebraic structure, which we aim to exploit in this project. A key ingredient in this context is the hierarchy of the so-called boundary maps and their adjoint co-boundary maps which couple higher-order to lower-order entities (e.g. edges to vertices). Combining these maps in an appropriate manner gives rise to higher-order Laplacian operators. The first order operator is the well-known graph Laplacian matrix, which is paramount for the analysis of networked systems. Like the graph Laplacian in the node domain, its higher order equivalents enable the rigorous definition of diffusive processes (random walks and consensus dynamics) in the domain of edges (node-pairs) and higher order entities [2].

[1] Benson, A. R.; Abebe, R.; Schaub, M. T.; Jadbabaie, A. & Kleinberg, J. “ Simplicial closure and higher-order link prediction” Proceedings of the National Academy of Sciences, 2018, DOI: 10.1073/pnas.1800683115
[2] Schaub, M. T.; Benson, A. R.; Horn, P.; Lippner, G. & Jadbabaie, A. “Random walks on simplicial complexes and the normalized Hodge 1-Laplacian”, SIAM Review, 2020. DOI: 10.1137/18M1201019

Flow decompositions, machine learning and signal processing on graphs and simplicial complexes

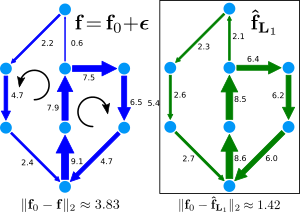image-right In many problems modeled using graphs, the data of interest is located on the edges (as opposed to the nodes). A typical scenario of practical interest is a flow on the edges – signal, mass, energy, information – of a graph that is measured and has to be analyzed further, such as traffic flow associated with the edges of a traffic network.

To analyze these types of signal we have developed techniques for analyzing the edge-space of graphs and simplicial complexes in more detail [1,2] An important tool in this context is the Hodge decomposition, a decomposition of edge flows into intuitively interpretable components that are analogous to notions such as gradient flows or rotational flows from vector calculus. We have demonstrated how this decomposition can be leveraged for data analytics that extract information about the edge-space that complements and extends typical graph-based analysis.

[1] Schaub, M. T.; Benson, A. R.; Horn, P.; Lippner, G. & Jadbabaie, A. “Random walks on simplicial complexes and the normalized Hodge 1-Laplacian”, SIAM Review, 2020. DOI: 10.1137/18M1201019
[2] Schaub M. T.; Segarra, S. “Flow smoothing and denoising: graph signal processing in the edge-space”. 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 2018, pp. 735-739. DOI: 10.1109/GlobalSIP.2018.8646701
[3] Jia, J.; Segarra, S.; Schaub, M. T. & Benson, A. R. “Graph-based Semi-Supervised & Active Learning for Edge Flows”. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2019), ACM, 2019 DOI: 10.1145/3292500.3330872

Presentations and Communication

Research related to the present project was presented at the following places / events.

  • Applied Topology Seminar, EPFL, Switzerland, February 2020
  • Department of Mathematics, University of Exeter, UK, January 2020
  • Computer Science Colloquium, RWTH Aaachen, Germany, January 2020
  • Complexity Oxford Imperial workship (COXIC 2019) , Imperial College London, UK, December 2019
  • Centre for Topological Data Analysis Meeting, University of Oxford, UK, November 2019
  • Control and Optimization Journal Club, University of Oxford, UK, October 2019
  • Networks Seminar, Mathematical Institute, University of Oxford, UK, October 2019
  • Algebra Statistics and Optimization Seminar, MIT, Cambridge MA, USA, April 2019
  • University Utrecht, Netherlands, April 2019.
  • University of Oxford, United Kingdom, March 2019.
  • Institute for Computational Biology, Helmholtz Zentrum München, Germany. February 2019.
  • FZ Juelich, Germany. December 2018.
  • Complex Networks 2018, Cambridge, United Kingdom, December 2018
  • Growth Lab Seminar, Center for International Development, Harvard University, Cambridge, USA, September 2018
  • PostDoc Lunch Seminar, Institute of Data, Systems and Society, MIT, Cambridge MA, USA, August 2018
  • International Conference on Complex Networks (ICCS) 2018, Boston MA, USA, July 2018
  • Imperial College London, Biomathematics Seminar, United Kingdom, November 2017
  • Netsci 2018 - Machine Learning in Network Science Workshop, Paris, France, June 2018
  • Netsci 2018, Paris, France, June 2018
  • Complenet 2018, Boston MA, USA, March 2018
  • University of Oxford, SysSoS group seminar, United Kingdom, November 2017
  • Université catholique de Louvain, Applied Mathematics Seminar / ICTEAM, Belgium, November 2017

Outreach

  • MIT Spark Programme, Cambridge, MA, March 2018
  • St. Ursula Gymnasium Bruehl, Outreach Talk, Germany, November 2017

Complete Publication list

A list of all publications that were produced during the period of the fellowship is given below.

  • Faccin M, Schaub MT and Delvenne J-C (2020), “State aggregations in Markov chains and block models of networks”, Physical Review Letters, Vol. 127(7), Aug. 2020 pp. 078301.
  • Schaub, M.T.; Segarra, S. & Tsitsiklis, J.N. (2020), “Blind identification of stochastic blockmodels from dynamical observations”, SIAM Journal on Mathematics of Data Science., May, 2020. Vol. 2(2), pp. 335-367.
  • Schaub, M.T.; Benson, A.R.; Horn, P.; Lippner, G. & Jadbabaie, A. (2020), “Random walks on simplicial complexes and the normalized Hodge 1-Laplacian”, SIAM Review., May, 2020. Vol. 62(2), pp. 353-391.
  • Neuhäuser L, Schaub MT, Mellor A and Lambiotte R (2020), “Opinion Dynamics with Multi-Body Interactions”, submitted. April, 2020.
  • Zhu, Y.; Schaub, M.T.; Jadbabaie, A. & Segarra, S. (2020), “Network Inference from Consensus Dynamics with Unknown Parameters”, IEEE Transactions on Signal and Information Processing over Networks., April, 2020. Vol. 6, pp. 300-315.
  • Roddenberry TM, Schaub MT, Wai H-T and Segarra S (2020), “Exact Blind Community Detection from Signals on Multiple Graphs”, submitted. January, 2020.
  • Avella-Medina, M.; Parise, F.; Schaub, M. & Segarra, S. (2020), “Centrality measures for graphons: Accounting for uncertainty in networks”, IEEE Transactions on Network Science and Engineering., January, 2020. Vol. 7(1), pp. 520-537.
  • Rosvall, M.; Delvenne, J.-C.; Schaub, M.T. & Lambiotte, R. (2019), “Different Approaches to Community Detection”, In Advances in Network Clustering and Blockmodeling., November, 2019. , pp. 105-119. John Wiley & Sons, Ltd.
  • Schaub, M.T.; Delvenne, J.-C.; Lambiotte, R. & Barahona, M. (2019), “Structured Networks and Coarse-Grained Descriptions”, In Advances in Network Clustering and Blockmodeling., November, 2019. , pp. 333-361. John Wiley & Sons, Ltd.
  • Jia, J.; Segarra, S.; Schaub, M.T. & Benson, A.R. (2019), “Graph-based Semi-Supervised & Active Learning for Edge Flows”, In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2019). New York, NY, USA, August, 2019. , pp. 761-771. ACM.
  • Schaub, M.T.; Delvenne, J.-C.; Lambiotte, R. & Barahona, M. (2019), “Multiscale Dynamical Embeddings of Complex Networks”, Phys. Rev. E., June, 2019. Vol. 99, pp. 062308. American Physical Society.
  • Schaub, M.T.; Segarra, S. & Wai, H. (2019), “Spectral Partitioning of Time-varying Networks with Unobserved Edges”, In 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2019)., May, 2019. , pp. 4938-4942.
  • Schaub, M.T. & Segarra, S. (2018), “Flow Smoothing And Denoising: Graph Signal Processing In The Edge-space”, In 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP)., November, 2018. , pp. 735-739.
  • Benson, A.R.; Abebe, R.; Schaub, M.T.; Jadbabaie, A. & Kleinberg, J. (2018), “Simplicial closure and higher-order link prediction”, Proceedings of the National Academy of Sciences., November, 2018. Vol. 115(48), pp. E11221-E11230.
  • Billeh, Y.N. & Schaub, M.T. (2018), “Feedforward architectures driven by inhibitory interaction patterns”, Journal of Computational Neuroscience., February, 2018. Vol. 44(1), pp. 63-74.
  • Faccin, M.; Schaub, M.T. & Delvenne, J.-C. (2017), “Entrograms and coarse graining of dynamics on complex networks”, Journal of Complex Networks., November, 2017. , pp. cnx055.
  • Estrada, E.; Delvenne, J.-C.; Hatano, N.; Mateos, J.L.; Metzler, R.; Riascos, A.P. & Schaub, M.T. (2017), “Random Multi-Hopper Model. Super-Fast Random Walks on Graphs”, Journal of Complex Networks., October, 2017. , pp. cnx043.

Contact

@MIT
Institute for Data, Systems, and Society
Massachusetts Institute of Technology
77 Massachusetts Avenue,
Office: E18-425C
Cambridge, MA, 02139

@Oxford
Department of Engineering Science
University of Oxford
Parks Road
Oxford, OX1 3PJ