Research
My research interests are broad, but have one common denominator: the use of networks to analyse a variety of systems and data. As networks have become an almost ubiquitous modeling tool in a range of different disciplines, this has enabled me to connect to a wide range of interdisciplinary applications. The modeling perspectives applied in these application areas can be quite different, however. My work may be partitioned into the following (overlapping) themes. For more details please also refer to Publications and Code.
For more information on my ERC project see HIGH-HOPeS.
For more information on my Marie Curie Project see HIntNets
Interdisciplinary Applications
One of the strengths of network models is their versatility: networks have become ubiquitous abstractions for social, physical, biological and engineered systems. Facilitated by my multidisciplinary background, I have been fortunate to work with great collaborators on a range of applications. I am particularly interested in biological problems, such as the analysis of neurophysiological data or the analysis of proteins and genetic data, but have also worked on applications concerning technical and social systems in the past.
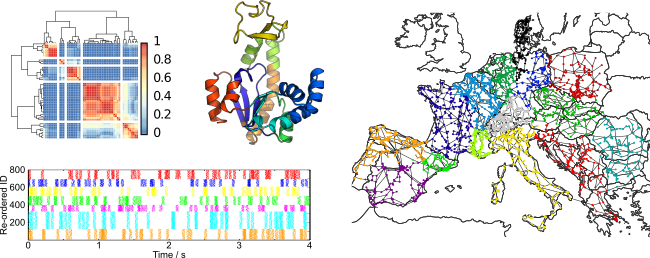
Modeling and analysing relational data as networks
One area in which networks have become prevalent is the modeling and analysis of relational data.
For instance, we may have data that measures social relations such as friendship between people.
Such data can be mapped into a network model by identifying people with nodes, and the (measured) relations between them as edges.
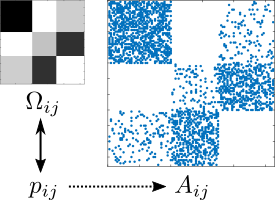
Since there is typically uncertainty about the present edges, we may have to adopt a statistical perspective towards the measured network topology and model it via a random graph model.
Many statistical challenges arise from the fact that we are typically confronted with \(n = 1\) observed network samples.
Some problems we are interested in within this domain is the identification of salient features in such a network, such as the identification of important nodes via centrality measures, or the detection of clusters (“communities”) and hierarchical structures potentially present in the network.
Dynamics and data on networks
In problems emerging from control theory and dynamical systems, we often consider a distributed dynamical system defined on a network structure. A similar view is also adopted in graph signal processing, in which the network defines the domain on which a signal is supported.
The object of interest is an (uncertain) signal defined on the nodes of the graph, e.g., a time-series for each node, or other types of measurements.
Our work focuses on understanding such dynamics and data in a more principled way by taking into account the underlying network structure. Problems of interest in this area include i) understanding the emergence of patterns in partially structured network, ii) model-order reduction and its links to graph clustering iii) inference of network structure from dynamics.
Simplicial complexes and higher-order network models
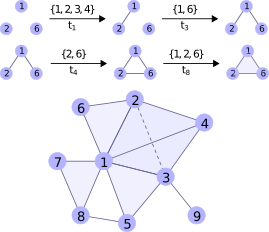Thus far, networks are mostly represented mathematically via graphs.
However, while graphs can capture pairwise interactions between nodes, fundamental interactions in networks often take place between multiple nodes.
For example, in a biochemical network a reaction often involves more than two species (\(A + B \rightarrow C + D\)), or two reagents might interact only in the presence of an enzyme.
In this line of research our goal is to investigate new types of models such as hypergraphs and simplicial complexes that account for interactions between groups of nodes (triplets, quadruplets, etc.). Questions of interest include:
- How can we analyse the effects of non-binary relationships on dynamical properties of networked systems?
- How can we design decentralized control and optimization strategies, utilizing such non-binary interactions?
- How can we utilize non-binary relationships for analysis of real world data, e.g., from biological networks?
Please also refer to my Marie Curie project HIntNets.